こんにちは、株式会社Key-Performanceの井畑です。
今回は、生産性を最大にするためのKPI設定の手法として、線形計画法の手順をご紹介します。
線形計画法とは??
・工場などの、「原料」「設備」「労働力」の分配によって、生産性が左右される場合に使う計画手法
・5万円の製品Aの個数をX1、8万円の製品Bの個数をX2とおいた時の最大の利益 M を求める場合、
「5X1 + 8X2 = M」 のような
利益の最大化を1次関数で求められる場合に使う。
・生産を制限する要素も一次不等式で表せる必要がある。
では、ここでは2種類の製品の生産をどんなふうに行うかを手計算で解いていきます。
ちなみに、3種類以上の製品でもこの線形計画法は使うことが出来ますが、とてもじゃないですが手計算では無理です。
3種類以上になった場合はおとなしくパソコンに頼りましょう笑
その場合は「シンプレックス法」というものを使います。
とりあえず今回は、2種類のものを例に、線形計画法でどのようにKPI設定を行うのかのイメージを掴んで下さい。
製品が2つだった場合の線形計画法の手順
例:ある工場での利益最大化:条件
【製品一つ当たりの利益】
製品A………5万円
製品B………8万円
【生産に必要な資源】
| 製品 | 原料 | 労働力 | 設備 |
| 製品A | 3Kg | 4人/時 | 6台/時 |
| 製品B | 10Kg | 6人/時 | 5台/時 |
【利用可能な資源】
原 料………440Kg
労働力………300人/時
設 備………350台/時
条件の一次式化
製品Aの生産個数をX1、製品Bの生産個数をX2とおくと、利益Mとの関係は次の式になる。
5X1 + 8X2 = M
※Aは5万円の利益になり、Bは8万円の利益になるから。
※利益Mは、一時間当たりの利益。
次に、利用可能な資源と生産に必要な資源を一次不等式で表すと、以下の3つの式になる。
・原料制約
3X1 + 10X2 ≦ 440 ………①
・労働力制約
4X1 + 6X2 ≦ 300 ………②
・設備制約
6X1 + 5X2 ≦ 350 ………③
(X1≧0、X2≧0)
※X1 も X2 も生産した製品の個数なので、マイナスになることはありえないです。
※なぜ①〜③がすべて不等式なのかというと、自社が持っている資源以上の生産は出来ないけれど、資源は使いきらなくてもいいからです。
条件の中でも利益の最大化
上の①〜③の不等式によって、X1、X2の範囲が制限されました。この範囲を満たしながら、利益Mを最大化する配分を見つけていきましょう。
中学校で習った連立方程式(不等式)の解き方で簡単に解けてしまいます。
(ちなみに、①〜③はすべて二元一次不等式なので、2つの式を比べることで解が得られます。今回は3つの式の中から2つを比べるので、比べる回数は3C2=3回です。)
【①と③を比べる】
①✕2ー③をすると、 15X2≦530 となるので、 X2≦35.33………
③✕2ー①をすると 9X1≦260 となるので X1≦28.88……
つまり、X1は28個が一番多い生産個数、X2は35個が一番多い生産個数となるのでMは………
(5✕28)+(8✕35)=420
一時間当たりに420万円の利益がでる計算となります。
しかし、ここで注意が必要です。今求めたX1とX2を②の式に代入すると………
(4✕28)+(6✕35)=322となります。
これでは労働力が322人必要です。
なので、①と③の式から導き出したX1、X2はこの条件の最適解にはなりませんでした。
同じように【②と③】、【①と②】をそれぞれ比べていきます。
(数学の解答をすることが目的ではないので、ここでは途中式を省略します。)
結果、【②と③】では、X1=37 X2=25となり、これは①の条件も満たしました。
【①と②】では、X1=16 X2=39となり、これは③を満たしました。
なので、利益を最大化する可能性のある配分はこの2つのどちらかです。
最後はそれぞれで出る利益を比べて見ましょう。
【②と③】の結果では、385万円の利益を生み出す事が出来ます。
【①と②】の結果では、392万円の利益を生み出す事が出来ます。
よって、今回の制約条件の中で利益を最大化する配分は
一時間当たりに製品Aを16個、製品Bを39個作る
となります。
なぜ線形計画法なのか??
では、なぜこの手法は「線形計画法」と呼ばれるのでしょうか??
上の①〜③をグラフ化すると以下のようになります。
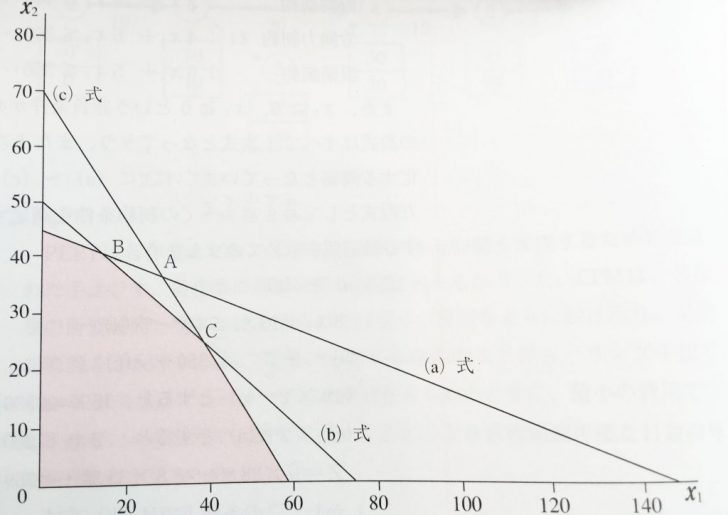
赤で塗りつぶされているところが選択出来る範囲でした。
そして、今求めた2つの不等式を同時に満たす解とは、グラフ上で言えば2つの直線の交点のことです。
なので、今回では【①と③】の交点Aは最初から範囲外なので候補に上がらず、【①と②】の交点Bか【②と③】の交点Cを考えればいいということがひと目でわかりました。
このように、直線のグラフの交点が最適解になるので、「線形計画法」なんです。
(本当はグラフに等利益線というものを引くと更に簡単になるのですが、ここでは割愛します。)
あとはKPI設定をするだけ
線形計画法によって、生産性を最大にする配分が明らかになりました。
あとは、この配分と目標生産量をしっかりと守れるように、各要素に対してKPIを設定していくだけです。
目標がはっきりしている分、KPIも精度の高い設定が出来ます。
※数値化の本領はここから※
ちょっとおまけです。
今回の例では、【①と③】を満たす配分では、②の条件を満たせませんでした。
では、その意味を考えて見ましょう。
なぜ【①と③】の配分ではだめだったのか??
②は労働力、つまり工場で働いている人の人数でした。この工場では1時間に300人の人が働いています。
もし【①と③】の条件を満たすためには、この工場で1時間に322人の人が働かなければいけません。
22人労働力が不足していた事が原因となり、【①と③】の配分は却下となります。
もし労働力が足りていたら??
今回は、制約条件を変えなかった場合の最適な配分を行った結果、392万円の利益が出ました。
もし、労働力が足りていた場合は、420万円の利益が出ることになりました。
この差は28万円。
つまりこの工場は、労働力が22人足りないせいで、28万円損をしていた事が判明しました。
もし、時給5000円で22人を雇ったとしても11万円の人経費です。
差し引き1時間に17万円ずつ利益が増えます。
時給5000円は限界まで高く見積もった金額ですので、実際にはこれの1/2〜1/5の金額になるでしょう。管理費や保険等を含めてもおそらく利益の向上が見込めます。
このように、数値化を行って予測を立てることで、様々な条件を比べ、最も利益の高くなる経営を行う事が出来ます。
まとめ
・線形計画法では最も利益の上がる配分を求める事が出来る
・求めた配分を達成するようにKPI設定を行うことで、KPIの精度が上がる
・数値化を行うことで、より利益が高くなる方法が見える事がある







コメントを残す